Traversing a Spiral Matrix
Manipulating data structures
1.0 Overview
Imagine navigating a 2D matrix like a winding staircase, traversing its elements in a continuous spiral. This intriguing pattern, known as spiral traversal, has applications in various domains, from image processing and data compression to game development and cryptography.
This blog post delves into the intricacies of spiral matrix traversal, guiding you through the logic and techniques required to effectively navigate a 2D array in this unique manner. We’ll use a classic LeetCode problem as a practical example, dissecting the problem statement and exploring an efficient algorithmic solution.
Whether you’re a seasoned programmer or just starting your coding journey, understanding spiral traversal will undoubtedly enhance your problem-solving toolkit and broaden your understanding of matrix manipulation. So, let’s unravel the spiral and explore this fascinating traversal technique together!
2.0 The usual traversal techniques
Before we dive into the intricacies of spiral traversal, let’s recap the common ways to navigate a 2D matrix. Typically, matrices are represented as multidimensional arrays, where each inner array corresponds to a row in the matrix. However, we can also utilize a single-dimensional array to store the matrix data, as long as we know the total number of rows and columns.
Let’s illustrate this with an example:
# 2D array representation matrix_2d = [ [1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12] ] # 1D array representation matrix_1d = [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12 ]
Both representations hold the same data, just organized differently. The matrix has 3 rows and 4 columns.
Traversing a 2D Array
To iterate through a 2D array, we use two nested loops: one for the rows and one for the columns.
total_rows = len(matrix_2d)
total_cols = len(matrix_2d[0])
for row in range(total_rows):
for col in range(total_cols):
print(matrix_2d[row][col])
This code snippet sequentially accesses each element in the matrix by iterating through each row and then each column within that row.
Traversing a 1D Array (representing a matrix)
When working with a 1D array that represents a matrix, we need to calculate the correct index based on the row and column position.
total_rows = 3
total_cols = 4
for row in range(total_rows):
for col in range(total_cols):
current_index = row * total_cols + col
print(matrix_1d[current_index])
# Mapping list index to matrix row and column
for i in range(len(matrix_1d)):
print(f"{i}, row: { i// total_cols}, col: {i % total_cols}")
Here, ‘row * total_cols + col’ effectively translates the row and column coordinates into the corresponding index in the 1D array.
Traversal Directions
We can traverse a matrix in various directions:
1. Horizontally: Increase (right) or decrease (left) the column index.
2. Vertically: Increase (down) or decrease (up) the row index.
3. Diagonally: Increase or decrease both the row and column indices simultaneously, depending on the desired diagonal direction.
Understanding these basic traversal techniques sets the stage for exploring more complex patterns like spiral traversal.
3.0 Traversing in a spiral structure
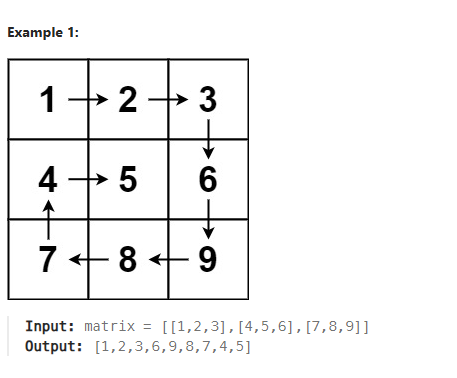
Our goal is to traverse the matrix with optimal efficiency, aiming for a linear time complexity of O(n). To achieve this, we’ll employ a technique that involves two key concepts:
1. The Terminal Condition
We halt the traversal process when all the cells surrounding our current position (left, right, up, and down) have been visited. This ensures that we cover every element in the matrix without redundancy.
2. Switching Directions
We initiate the traversal by moving rightward. Upon encountering the boundary of the matrix or a previously visited cell, we strategically switch our direction as follows:
a. Right to Down: When we can no longer move right, we shift our direction downwards.
b. Down to Left: Upon reaching the last available row in the current column, we reverse direction and start moving left.
c. Left to Up: When we hit the first available column in the current row, we switch direction again and move upwards.
d. Up to Right: Finally, upon reaching the topmost available position in the current column, we complete the cycle by switching back to moving right.
This cyclical pattern of direction switching allows us to navigate the matrix in a spiral fashion until we satisfy the terminal condition.
Required actions
To implement this spiral traversal, we need to determine the validity of each potential move:
1. Move Right: We can move right if the cell to the right of our current position is unvisited or if we’ve reached the end of the current row.
def to_index(row, col, total_cols):
return row * total_cols + col
def can_move_right(visited, current_row, current_col, total_rows, total_cols):
right_index = to_index(current_row, current_col+1, total_cols)
return current_col + 1 < total_cols and not visited[right_index]
2. Move left: We can move left if the cell to the left of our current position is unvisited or if we’ve reached the beginning of the current row.
def can_move_left(visited, current_row, current_col, total_rows, total_cols):
left_index = to_index(current_row, current_col-1, total_cols)
return current_col - 1 >= 0 and not visited[left_index]
3. Move down: We can move down if the cell below our current position is unvisited or if we’ve reached the end of the current column.
def can_move_down(visited, current_row, current_col, total_rows, total_cols):
down_index = to_index(current_row + 1, current_col, total_cols)
return current_row + 1 < total_rows and not visited[down_index]
4. Move up: We can move up if the cell above our current position is unvisited or if we’ve reached the beginning of the current column.
def can_move_up(visited, current_row, current_col, total_rows, total_cols):
up_index = to_index(current_row - 1, current_col, total_cols)
return current_row - 1 >= 0 and not visited[up_index]
Required Variables
To effectively traverse the matrix in a spiral order, we need to keep track of several key pieces of information:
def spiralOrder(matrix):
"""
This function traverses a matrix in spiral order and returns the list of elements.
@param matrix List[List[int]]: The matrix items
"""
total_rows = len(matrix)
total_cols = len(matrix[0])
# Current index being traversed
current_row = 0
current_col = 0
# Start by moving right. Available directions: l (left), r (right), u (up), d (down)
current_direction = 'r'
# List of cells visited
visited = [False] * (total_rows * total_cols)
# keep track if we can move in the direction - Initially start by moving right
move_right = True
move_left = False
move_down = False
move_up = False
In this code:
1. total_rows and total_cols store the dimensions of the matrix.
2. current_row and current_col maintain the current position during traversal.
3. current_direction indicates the current direction of movement (‘r’ for right, initially).
4. visited is a boolean list that tracks whether each cell has been visited.
5. move_right, move_left, move_down, and move_up are boolean flags that control the allowed directions of movement.
Visiting each cell
Now, let’s delve into the core loop that iterates through the matrix:
# while all elements around it have not been visited
while move_right or move_left or move_down or move_up:
move_right = can_move_right(visited, current_row, current_col, total_rows, total_cols)
move_left = can_move_left(visited, current_row, current_col, total_rows, total_cols)
move_down = can_move_down(visited, current_row, current_col, total_rows, total_cols)
move_up = can_move_up(visited, current_row, current_col, total_rows, total_cols)
index = to_index(current_row, current_col, total_cols)
result.append(matrix[current_row][current_col])
visited[index] = True
This while loop continues as long as there’s at least one possible direction to move to an unvisited adjacent cell. Inside the loop:
1. We check if moving in each direction (right, left, down, up) is valid using helper functions like can_move_right (which you’ll define later).
2. to_index (another helper function) converts the current row and column to the corresponding index in the visited list.
3. The current cell’s value is added to the result list.
4. The current cell is marked as visited in the visited list.
This sets the stage for the implementation of the helper functions and the direction-switching logic within the loop, which will complete the spiral traversal algorithm.
Choosing the next step
The core of our spiral traversal algorithm lies in determining the next cell to visit and adjusting the direction of movement accordingly. We achieve this through a series of conditional checks based on the current_direction:
if current_direction == 'r': # We are currently moving right if move_right: # can move right current_col += 1 continue elif move_down: # Change direction current_row += 1 current_direction = 'd' continue else: # Cannot move in the intended direction break elif current_direction == 'd': # We are currently moving down if move_down: current_row += 1 continue elif move_left: # Change direction current_col -= 1 current_direction = 'l' continue else: # Cannot move in the intended direction break elif current_direction == 'l': # We are currently moving left if move_left: current_col -= 1 continue elif move_up: # Change direction current_row -= 1 current_direction = 'u' continue else: # Cannot move in the intended direction break elif current_direction == 'u': # We are currently moving up if move_up: current_row -= 1 continue elif move_right: # Change direction current_col += 1 current_direction = 'r' continue else: # Cannot move in the intended direction break
In each if block, we first check if we can continue moving in the current_direction. If so, we update current_row or current_col accordingly and continue to the next iteration of the loop.
If we cannot continue in the current direction, we check if it’s possible to change direction (e.g., from right to down). If a direction change is valid, we update current_direction and the corresponding row or column index, then continue.
If neither continuing in the current direction nor changing direction is possible, it indicates that we’ve completed the spiral traversal, and we break out of the loop.
This logic ensures that we systematically navigate the matrix in a spiral pattern, changing direction only when necessary to maintain the spiral path.
The complete code is as follows:
def to_index(row, col, total_cols):
return row * total_cols + col
def can_move_right(visited, current_row, current_col, total_rows, total_cols):
right_index = to_index(current_row, current_col+1, total_cols)
return current_col + 1 < total_cols and not visited[right_index]
def can_move_left(visited, current_row, current_col, total_rows, total_cols):
left_index = to_index(current_row, current_col-1, total_cols)
return current_col - 1 >= 0 and not visited[left_index]
def can_move_down(visited, current_row, current_col, total_rows, total_cols):
down_index = to_index(current_row + 1, current_col, total_cols)
return current_row + 1 < total_rows and not visited[down_index]
def can_move_up(visited, current_row, current_col, total_rows, total_cols):
up_index = to_index(current_row - 1, current_col, total_cols)
return current_row - 1 >= 0 and not visited[up_index]
def spiralOrder(matrix):
"""
This function traverses a matrix in spiral order and returns the list of elements.
@param matrix List[List[int]]: The matrix items
"""
result = []
if len(matrix) == 0:
return result
total_rows = len(matrix)
total_cols = len(matrix[0])
if total_cols == 0:
return result
current_row = 0
current_col = 0
current_direction = 'r'
visited = [False] * (total_rows * total_cols)
move_right = True
move_left = False
move_down = True
move_up = False
while move_right or move_left or move_down or move_up:
move_right = can_move_right(visited, current_row, current_col, total_rows, total_cols)
move_left = can_move_left(visited, current_row, current_col, total_rows, total_cols)
move_down = can_move_down(visited, current_row, current_col, total_rows, total_cols)
move_up = can_move_up(visited, current_row, current_col, total_rows, total_cols)
index = to_index(current_row, current_col, total_cols)
result.append(matrix[current_row][current_col])
visited[index] = True
if current_direction == 'r':
if move_right:
current_col += 1
continue
elif move_down:
current_row += 1
current_direction = 'd'
continue
else:
break
elif current_direction == 'd':
if move_down:
current_row += 1
continue
elif move_left:
current_col -= 1
current_direction = 'l'
continue
else:
break
elif current_direction == 'l':
if move_left:
current_col -= 1
continue
elif move_up:
current_row -= 1
current_direction = 'u'
continue
else:
break
elif current_direction == 'u':
if move_up:
current_row -= 1
continue
elif move_right:
current_col += 1
current_direction = 'r'
continue
else:
break
break
return result
matrix = [
[1,2,3,4],
[5,6,7,8],
[9,10,11,12],
[13,14,15,16],
[17,18,19,20],
[21,22,23,24]
]
print(spiralOrder(matrix))
# Output: [1, 2, 3, 4, 8, 12, 16, 20, 24, 23, 22, 21, 17, 13, 9, 5, 6, 7, 11, 15, 19, 18, 14, 10]
4.0 Conclusion
In this blog post, we embarked on a journey to unravel the intricacies of spiral matrix traversal. We explored the fundamental concepts behind this technique, dissecting the logic and steps involved in navigating a 2D array in a spiral pattern. By leveraging a classic LeetCode problem as our guide, we demonstrated how to translate these concepts into a working algorithm, complete with code examples and explanations.
Mastering spiral traversal equips programmers with a valuable tool for solving a variety of problems involving 2D matrices. From image processing and data compression to game development and pathfinding, this technique finds applications in diverse domains. By understanding the principles and implementation details discussed in this post, you’re now well-prepared to tackle challenges that demand efficient and systematic matrix navigation.
As you continue your programming journey, remember that exploring different traversal techniques broadens your problem-solving horizons. So, keep experimenting, keep learning, and continue to unlock the fascinating world of algorithms and data structures!